Two Rex Makes #9 - Power Curve
We’ve made good progress with our game over the last few weeks after switching it from a space combat game into a factory builder (there are more similarities than you might think!). It’s essentially a flip & write where you’re gathering resources to construct fantastical equipment that produces and distributes a range of sweets.
Now that we’re happy with much of the basic gameplay we’ve been spending some time building out the deck of cards which provide variety in the building components. Coming up with ideas hasn’t been a problem as the new theme has been fertile ground for interesting buildings that would thematically work in a magic candy factory. But generating a lot of cards has meant that we’ve had to start thinking about balancing issues which we’re doing using a combination of our own play testing and trying out a more mathematical approach using a power curve.
Constructing a Power Curve
So, what’s our understanding of a power curve and how did we go about constructing it? A power curve is a simple model that summarises the ‘cost’ and ‘power’ of each card on a numerical scale, so you can easily compare each card in the deck. In their broadest terms, ‘cost’ is what you need to get the card into play, and power is what you get back from the card once it’s out.
As soon as you give any serious thought to summarising a card’s cost and power you quickly realise this it’s impossible to capture everything, so it’s going to be a pragmatic approach which is as much of an art as a science. The first picture below shows a sample card for “Scooter Puffs”, a factory on wheels which churns out sugary breakfast cereal. The top right-hand corner gives the cost - two coins and two magic which are our basic resource types (thematically, the idea is that coins buy you more mundane items and magic allows you to purchase far-fetched ones).
Coins are relatively easy to come by, but magic is a trickier resource to generate, so we assign a ratio between the two, so that one magic resource is equivalent to three coins. Why 3:1 and not 5:1? Simply judgement on how much more difficult it is to accrue the right resource type – there’s nothing more precise going on behind the scenes.
But these are just the explicit costs. There are also implicit ones such as how difficult it is to place on the grid. Size is one aspect of placement as the grid you’re working on is of limited size, so the bigger the footprint of the component, the more restrictions you’ll face. So, it seems fair to assign a big card a higher ‘cost’ than a card with a smaller area. Scooter Puffs for example is a medium sized card.
But there’s another dimension to consider around difficulty to place. Each component needs to be connected to the rest of your factory and some cards have obstacles on them which make this harder to do. Scooter Puffs is a thin corridor which makes it trickier to make connections, so this is one of the harder cards to place.
We assessed each card’s difficulty to place against on a scale of 1 (easy to place) to 5 (very difficult), judgementally considering both size and obstacles on that card but with some basic guidance to help with consistency when making selections. Continuing the Scooter Puffs example, we ranked it as a ‘4’ on this scale mainly due to the awkwardness n getting it to connect to the rest of the factory.
We went through a similar process with the ‘reward’ side of the equation. That’s even tougher, as some of our cards link together to form a reward engine, so assessing them in isolation can be misleading.
Using the curve
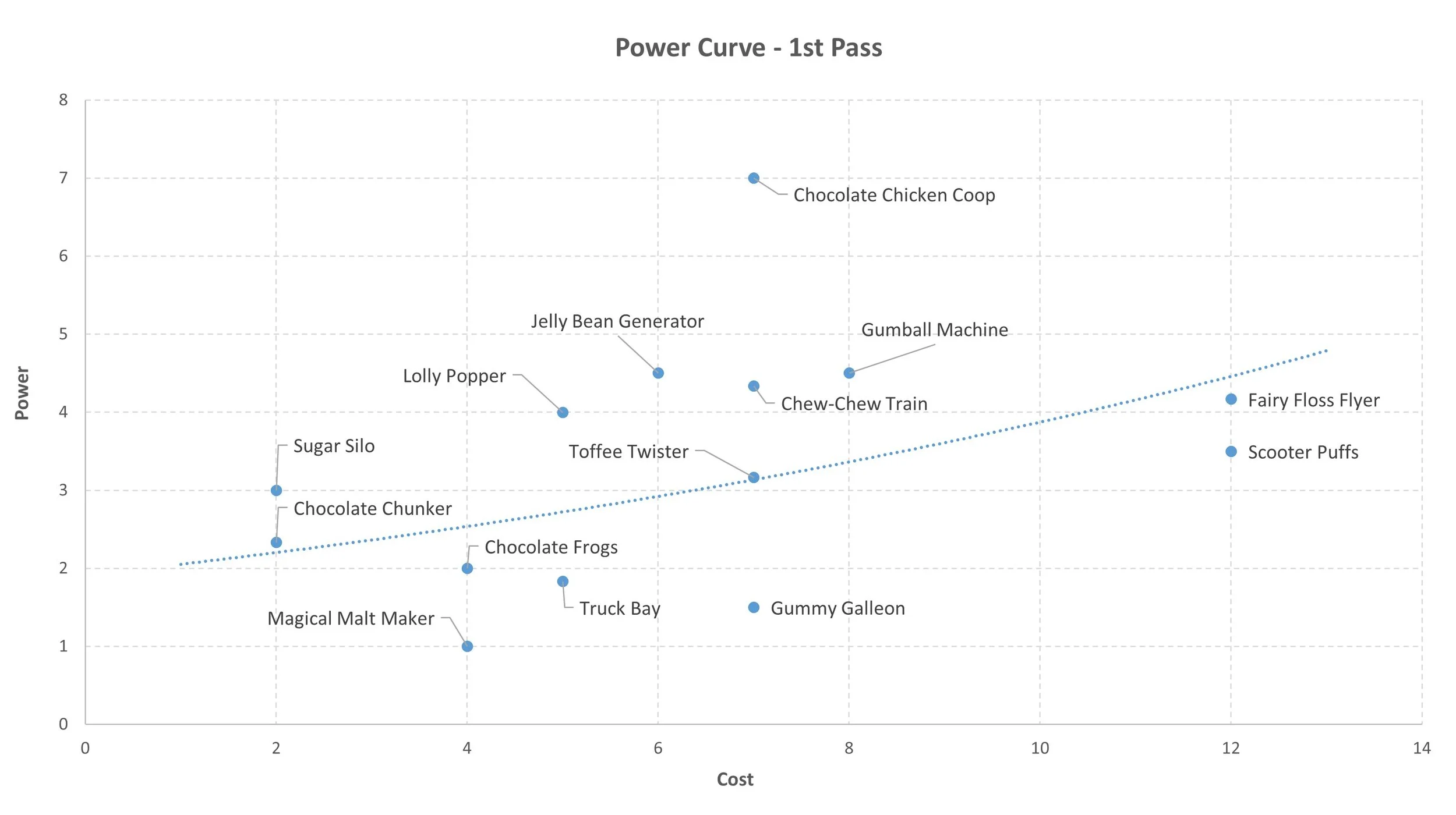
After assigning a cost and power to each card, you can plot them on a graph to visualise how the entire deck stacks up. There’s a picture of the first cut of this in the gallery on our blog.
The graph shows the results from the set of cards which had been designed ‘by eye’ without much play testing, so it was interesting to see that by and large we’d got the right association between cost and reward. The dotted line shows is a line of best fit from these cards and represents the power curve and has the following interesting features:
You can assess whether there are any obvious outliers (overpowered or underpowered cards). There are a couple of these – the Chocolate Chicken Coop looks significantly overpowered and the Gummy Galleon, Truck Bay, and Magical Malt Maker are all underpowered. When we play tested the game shortly afterwards, I was sure to nab the overpowered card when it came out of the pack, and it did feel like it gave far too much reward for a mid-level cost of card.
You can assess whether the power curve (the dotted line) is increasing linearly or exponential. In this first pass it’s basically a straight line which means a high-cost card could be replaced with several low-cost cards and you would get the same overall reward. Put another way, you get the same bang for your buck if you’re only spending one dollar or one hundred.
If the power curve is exponential rather than linear, the high-cost cards would outperform the low-cost ones, so you’re better off with a high-cost card than a series of small ones. Most games aim for an exponential power curve, with a common argument that in order afford the higher cost card you need to horde resources which means you’re giving up the opportunity to buy & benefit from lower cost cards, and that’s not allowed for in the model (so it’s ‘fair’ that these give more reward once they are in play).
For our game, that argument doesn’t quite stack up for gameplay reasons which are specific to the design – you’re meant to be purchasing something every turn in order to grow your engine to give enough additional resource for a high-powered card. But we still want the power curve to be exponential as it’s a short experience that’s going to restrict the high-power cards until the tail end of the game when they will only be in play for a few turns. So, we want these to feel like powerful cards that will give a big boost for a few turns towards the end of the game. As a result of this first pass we nerfed and buffed a few of the existing cards to eliminate outliers, but we also introduced some special power cards for end-game play - see the second sample card above called “Jelly Bean Cannon”. These are expensive to acquire but give significant rewards and help the power curve to take an exponential shape:
Now it really is a curve, and whilst there are still outliers there are fewer of them.
Closing Thoughts
Do you want everything perfectly on the power curve? We’ve probably got enough levers to pull that we could just about do this if we wanted, but we’re going to consciously allow for some variance. This is partially a recognition that the ‘power’ doesn’t capture everything, some cards may look underpowered in isolation but can combine well with others to make strong resource generating engines. We’re not going to try and capture that in the power curve model, but we will look to have a good reason why some cards are off the curve.
What else did we learn?
Our instinctual design wasn’t too far off, but the power curve was good at identifying couple of outliers at an early stage – it’s likely that we would have come to his conclusion through play testing, but this was certainly a quicker way to get there. But when you’re quickly swapping card ideas in and out of the game, it’s a really useful tool to help get you started & save play testing time.
Designing the exponential growth in the curve was harder and it didn’t look like we got that right, and again the power curve was helpful at delivering that message early on.
There’s no substitute for actual play testing, and no power curve model is going to fully capture every aspect of how a particular card works. At some level human intuition and experience will trump mathematics.
Interested in learning more about power curves? Here are some of the online resources we used when researching the topic – they are mainly focussed on trading card games, but we think that many of the same principles apply to broader game types:
https://www.cloudfallstudios.com/blog/2018/5/14/design-tips-power-curves-i